polígonos convexos. Definición de un polígono convexo. Las diagonales de un polígono convexo

Estas formas geométricas están a nuestro alrededor. polígonos convexos son naturales, como un panal o artificial (hecho por el hombre). Estas cifras se utilizan en la producción de diferentes tipos de recubrimientos en el arte, la arquitectura, adornos, etc. polígonos convexos tienen la propiedad de que sus puntos se encuentran en un lado de una línea recta que pasa a través del par de vértices adyacentes de la figura geométrica. Hay otras definiciones. Se llama el polígono convexo, que está dispuesto en un solo semiplano con respecto a cualquier línea recta que contiene de uno de sus lados.

polígonos convexos

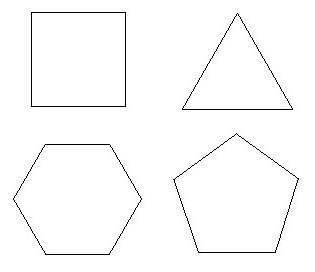En el curso de la geometría elemental siempre son tratados polígonos extremadamente simples. Para entender las propiedades de formas geométricas que necesita para comprender su naturaleza. Para empezar a entender que es cerrado cualquier línea cuyos extremos son los mismos. Y la figura formada por ella, puede tener una variedad de configuraciones. Polygon se llama polilínea cerrada simple cuyas unidades adyacentes no están situada en una línea recta. Sus enlaces y nodos son, respectivamente, los lados y la parte superior de la figura geométrica. Una línea poligonal simple no debe cortarse consigo mismo.

vértices del polígono se llaman los vecinos, en caso de que son los extremos de uno de sus lados. Una figura geométrica, que tiene un número n-ésimo de vértices, y por lo tanto el número n-ésimo de los partidos llamados el n-gon. Misma línea de trazos es el límite o contorno de la figura geométrica. plano poligonal o polígono plano llamado la parte final de cualquier plano, su limitado. lados adyacentes de la figura geométrica llamados segmentos de polilínea procedentes de la misma vértice. No serán vecinos si se basan en diferentes vértices del polígono.

Otras definiciones de polígonos convexos

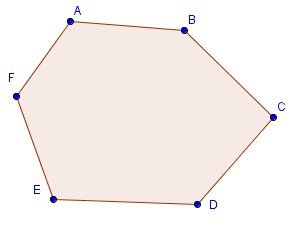En geometría elemental, hay varios equivalente en las definiciones de sentido, lo que indica lo que se llama un polígono convexo. Además, todas estas afirmaciones son igualmente verdaderas. Un polígono convexo es la que tiene:

• cada segmento que conecta dos puntos cualesquiera dentro de ella, se encuentra por completo en él;

• mentir en él todas sus diagonales;

• cualquier ángulo interior no es mayor que 180 °.

Polygon siempre divide el plano en dos partes. Uno de ellos – el limitado (se puede encerrar en un círculo), y el otro – ilimitado. El primero se llama la región interior, y el segundo – el área exterior de la figura geométrica. Esta es la intersección del polígono (en otras palabras – el componente total) varios semiplanos. Por lo tanto, cada segmento tiene extremos en los puntos que pertenecen a un polígono pertenece completamente a él.

Variedades de polígonos convexos

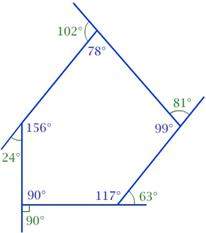Definición polígono convexo no indica que hay muchas clases de ellos. Y cada uno de ellos tiene ciertos criterios. Por lo tanto, los polígonos convexos, que tienen un ángulo interno de 180 °, que se refiere ligeramente convexo. La figura geométrica convexa que tiene tres picos, se llama un triángulo, cuatro – cuadrilátero, cinco – pentágono, etc. Cada uno de los convexa n-gons cumple con los siguientes requisitos importantes: .. N debe ser igual o mayor que 3. Cada uno de los triángulos es convexa. La figura geométrica de este tipo en el que todos los vértices están situados en un círculo, llamado el círculo inscrito. Descrito polígono convexo se llama si todos sus lados alrededor de un círculo de tocarla. Dos polígonos se llaman igual sólo en el caso cuando se utiliza el recubrimiento se puede combinar. polígono plano llamado plano poligonal (una porción plana) que esta figura geométrica limitada.

polígono regular convexo

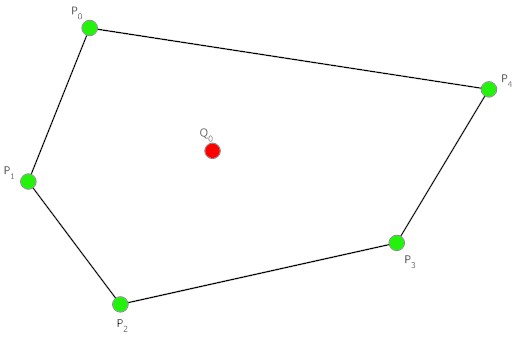polígonos regulares llamados formas geométricas con ángulos iguales y los lados. Dentro de ellos hay un punto 0, que es la misma distancia de cada uno de sus vértices. Se llama el centro de la figura geométrica. Las líneas que conectan el centro con los vértices de la figura geométrica llamados apotema, y los que conectan el punto 0 con las partes – radios.

Correcta rectángulo – cuadrado. triángulo equilátero se llama equilátero. Para tales formas no es la regla siguiente: cada ángulo polígono convexo es 180 ° * (n-2) / n,

donde n – número de vértices de la figura geométrica convexa.

El área de cualquier polígono regular se determina por la fórmula:

S = P * h,

donde p es igual a la mitad de la suma de todos los lados del polígono, y h es la apotema longitud.

Propiedades de los polígonos convexos

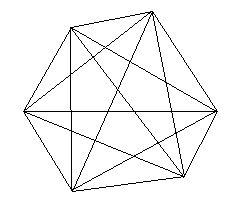polígonos convexos tienen ciertas propiedades. Por lo tanto, el segmento que une dos puntos cualesquiera de una figura geométrica, necesariamente situado en ella. la prueba:

Supongamos que P – el polígono convexo. Tomar dos puntos arbitrarios, por ejemplo, A y B, que pertenecen a P. Por la definición actual de un polígono convexo, estos puntos se encuentran en un lado de la línea recta que contiene cualquier dirección R. Por consiguiente, AB también tiene esta propiedad y está contenida en R. Un polígono convexo siempre puede dividirse en varios triángulos absolutamente todas las diagonales, que celebró uno de sus vértices.

Los ángulos formas geométricas convexas

Los ángulos de un polígono convexo – son los ángulos que se forman por las partes. Las esquinas interiores están en el área interior de la figura geométrica. El ángulo que se forma por los lados que convergen en un vértice, llamado el ángulo del polígono convexo. Esquinas adyacentes a las esquinas internas de la figura geométrica, llamada externa. Cada esquina de un polígono convexo, dispuesto en su interior, es:

180 ° – x

donde x – valor fuera de la esquina. Esta sencilla fórmula es aplicable a cualquier tipo de formas geométricas tales.

En general, para las esquinas exteriores existen siguiente regla: cada ángulo polígono convexo igual a la diferencia entre 180 ° y el valor del ángulo interior. Puede tener valores que van desde -180 ° a 180 °. En consecuencia, cuando el ángulo interior es 120 °, el aspecto tendrá un valor de 60 °.

La suma de los ángulos de los polígonos convexos

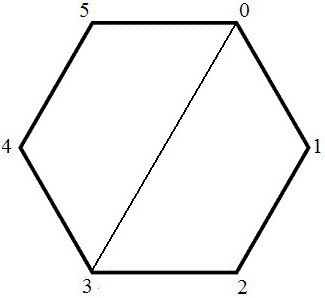La suma de los ángulos interiores de un polígono convexo se establece por la fórmula:

180 ° * (n-2),

donde n – número de vértices de la n-gon.

La suma de los ángulos de un polígono convexo se calcula sencillamente. Considere cualquier forma geométrica. Para determinar la suma de los ángulos de un polígono convexo que tenga que conectar uno de sus vértices a otros vértices. Como resultado de esta acción se convierte (n-2) del triángulo. Se sabe que la suma de los ángulos de cualquier triángulo es siempre 180 °. Debido a su número en cualquier polígono es igual a (n-2), la suma de los ángulos interiores de la figura es igual a 180 ° x (n-2).

Monto esquinas polígono convexo, es decir, cualquiera de los dos ángulos internos y externos adyacentes a ellos, en este figura geométrica convexa siempre será igual a 180 °. Sobre esta base, podemos determinar la suma de todos sus rincones:

180 x n.

La suma de los ángulos interiores es 180 ° * (n-2). Por consiguiente, la suma de todas las esquinas exteriores de la Figura conjunto por la fórmula:

180 ° * n-180 ° – (N-2) = 360 °.

Suma de los ángulos externos de cualquier polígono convexo siempre será igual a 360 ° (independientemente del número de sus lados).

de esquina exterior de un polígono convexo se representan generalmente por la diferencia entre 180 ° y el valor del ángulo interior.

Otras propiedades de un polígono convexo

Además de las propiedades básicas de las figuras geométricas de datos, sino que también tienen otra, que se producen cuando el manejo de ellos. Por lo tanto, cualquiera de los polígonos se podrán dividir en múltiples convexa n-gons. Para hacer esto, continúe a cada uno de sus lados y cortar la forma geométrica a lo largo de estas líneas rectas. Dividir cualquier polígono en varias partes convexas es posible y de modo que la parte superior de cada una de las piezas coinciden con todos sus vértices. A partir de una figura geométrica puede ser muy sencillo de hacer triángulos a través de todas las diagonales desde un vértice. Por lo tanto, cualquier polígono, en última instancia, puede ser dividido en un cierto número de triángulos, que es muy útil para resolver diversas tareas relacionadas con este tipo de formas geométricas.

El perímetro del polígono convexo

Los segmentos de la polilínea, polígono partes llamados, a menudo indican con las letras siguientes: AB, BC, CD, DE, EA. Este lado de una figura geométrica con vértices a, b, c, d, e. La suma de las longitudes de los lados de un polígono convexo se llama su perímetro.

La circunferencia del polígono

polígonos convexos pueden ser introducidos y descritos. Círculo tangente a todos los lados de la figura geométrica, llamada inscrito en él. Este polígono se llama descrito. El círculo central que se inscribe en el polígono es un punto de intersección de las bisectrices de los ángulos dentro de una forma geométrica dada. El área del polígono es igual a:

S = p * r,

donde r – el radio del círculo inscrito, y p – semiperímetro este polígono.

Un círculo que contiene los vértices del polígono, llamado describe cerca de él. Por otra parte, esta figura geométrica convexa llamada inscrito. El centro de círculo, que se describe sobre un polígono de este tipo es un denominado punto de intersección midperpendiculars todos los lados.

Diagonal formas geométricas convexas

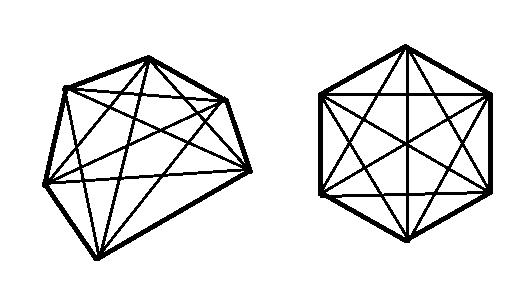Las diagonales de un polígono convexo – un segmento que no conecta vértices vecinos. Cada uno de ellos es el interior de esta figura geométrica. El número de diagonales de la n-gon se establece de acuerdo con la fórmula:

N = n (n – 3) / 2.

El número de diagonales de un polígono convexo juega un papel importante en la geometría elemental. El número de triángulos (K), que puede romper cada polígono convexo, calculado por la siguiente fórmula:

K = n – 2.

El número de diagonales de un polígono convexo es siempre dependiente del número de vértices.

Partición de un polígono convexo

En algunos casos, para resolver tareas geometría necesaria para romper un polígono convexo en varios triángulos con diagonales no entrecruzadas. Este problema puede ser resuelto mediante la eliminación de una cierta fórmula.

Definición del problema: llamar tipo de partición de un polígono regular convexo en varios triángulos diagonales que se cruzan solamente en los vértices de una figura geométrica.

Solución: Supongamos que P1, P2, P3, …, Pn – la parte superior de la n-gon. Número Xn – el número de sus particiones. Considere cuidadosamente la diagonal resultante figura geométrica Pi Pn. En cualquiera de las particiones regulares P1 Pn pertenece a un triángulo particular, P1 Pi Pn, en la que 1 <i <n. Basado en esto y suponiendo que i = 2,3,4 …, n-1, obtenido por (n-2) de estas particiones, que se incluyen en cada posibles casos especiales.

Sea i = 2 es un grupo de particiones regulares, siempre que contiene diagonal P2 Pn. El número de particiones que se incluyen en ella, igual al número de particiones (n-1) -gon S2 S3 S4 … Pn. En otras palabras, es igual a Xn-1.

Si i = 3, entonces las otras particiones grupo siempre contener una diagonal P3 P1 y P3 Pn. El número de particiones correctas que están contenidos en el grupo, coincidirá con el número de particiones (n-2) -gon P3, P4 … Pn. En otras palabras, será Xn-2.

Sea i = 4, entonces los triángulos entre la partición correcta está obligado a contener un triángulo P1 Pn P4, que lindan con el cuadrángulo P1 P2 P3 P4, (n-3) -gon P5 P4 … Pn. El número de particiones correctas tales cuadrilátero es igual a X4, y el número de particiones (n-3) es igual a -gon Xn-3. Con base en lo anterior, podemos decir que el número total de particiones regulares que están contenidos en este grupo es igual a 3 Xn-X4. Otros grupos, en el que i = 4, 5, 6, 7 … contendrá 4 Xn-X5, Xn-5 X6, Xn-6 … X7 particiones regulares.

Sea i = n-2, el número de particiones correctas en un grupo dado coincidirá con el número de particiones en el grupo, en el que i = 2 (en otras palabras, es igual a Xn-1).

Desde X1 = X2 = 0, X3 = 1 y X4 = 2, …, el número de particiones de polígono convexo es:

Xn = Xn-1 + Xn-2 + Xn-3, Xn-X4 + X5 + 4 … + X 5 + 4 Xn-Xn-X 4 + 3 + 2 Xn-Xn-1.

ejemplo:

X5 = X4 + X3 + X4 = 5

X6 = X4 + X5 + X4 + X5 = 14

X7 + X5 = X6 + X4 * X4 + X5 + X6 = 42

X7 = X8 + X6 + X4 X5 * + X4 X5 * + X6 + X7 = 132

El número de particiones correctas de intersección dentro de una diagonal

Tras un análisis de los casos individuales, se puede suponer que el número de diagonales de convexa n-gon es igual al producto de todas las particiones de este patrón gráfico (n-3).

La prueba de esta hipótesis: supongamos que P1n = Xn * (n-3), entonces cualquier n-gon se puede dividir en (n-2) es un triángulo. En este caso uno de ellos se pueden apilar (n-3) -chetyrehugolnik. Al mismo tiempo, cada cuadrilátero es diagonal. Desde esta figura geométrica convexa dos diagonales pueden llevarse a cabo, lo que significa que en cualquier (n-3) -chetyrehugolnikah pueden realizar adicional diagonal (n-3). Sobre esta base, se puede concluir que en cualquier partición adecuada tiene la oportunidad de (n-3) -diagonali reunión con los requisitos de esta tarea.

Zona de polígonos convexos

A menudo, en la solución de diversos problemas de geometría elemental existe la necesidad de determinar el área de un polígono convexo. Supóngase que (Xi. Yi), i = 1,2,3 … n representa una secuencia de coordenadas de todos los vértices vecinos del polígono, que no tiene auto-intersecciones. En este caso, su área se calcula por la siguiente fórmula:

_{S = ½ (Σ (X i} + X i + ₁₎ (Y _{i +} y _i + _1)),

en donde (X _1, Y _{1) = (X n 1, Y} n + _1).