Representación de números en un ordenador. Representación de números enteros y números reales en la memoria del ordenador

Cualquiera que haya pensado en mi vida que se convierta en el "pro" o administrador del sistema, o simplemente para vincular el lote con la tecnología informática, el conocimiento acerca de cómo la representación de los números en la memoria del ordenador es absolutamente necesario. Después de todo, en base a estos lenguajes de programación de bajo nivel como ensamblador. Por lo tanto, hoy en día tenemos en cuenta la representación de los números en el ordenador y colocarlos en las células de memoria.

notación

Si usted está leyendo este artículo, es probable que ya se sabe sobre él, pero vale la pena repetir. Todos los datos en un ordenador personal se almacenan en el binario sistema numérico. Esto significa que cualquier número que debe presentar el formulario correspondiente, que se compone de ceros y unos.

Con el fin de transferir habitual para nosotros números decimales a un ordenador comprensible forma, debe utilizar el algoritmo se describe a continuación. También hay calculadoras especializadas.

Por lo tanto, con el fin de poner el número en el sistema binario, es necesario tomar nuestro valor elegido y se divide por 2. Después de esto, obtenemos el resultado y el resto (0 ó 1). Resultado 2 de nuevo dividir y memorizar residuo. Este procedimiento debe repetirse siempre que el resultado también será 0 o 1. A continuación, escriba el valor final y los restos en el orden inverso, tal como los hemos recibido.

Eso es exactamente lo que está sucediendo en la representación informática de números. Cualquier número almacenado en forma binaria, y luego tomar la celda de memoria.

memoria

Como usted ya debe saber la unidad de información mínima es de 1 bit. Como hemos visto, la representación de los números en el ordenador se realiza en formato binario. Por lo tanto, cada bit de la memoria está ocupada por un valor de – 1 o 0.

Para el almacenamiento de un gran número utilizado célula. Cada unidad contiene 8 bits de información. Por lo tanto, podemos concluir que el valor mínimo en cada segmento de memoria puede ser 1 o ser un número binario de ocho bytes.

todo

Finalmente llegamos a la colocación directa de datos en un ordenador. Como se ha mencionado, la primera cosa que el procesador traduce la información en un formato binario, y sólo entonces se asigna la memoria.

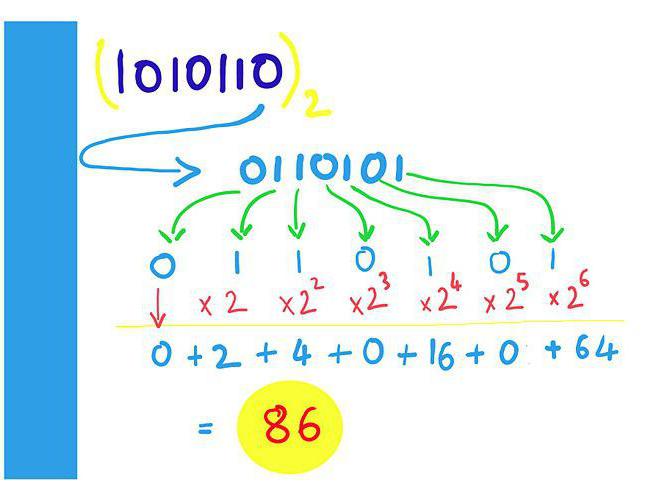
Vamos a empezar con la opción más sencilla, que es la representación de números enteros en el ordenador. memoria de la PC se asigna para el proceso es ridículamente pequeño número de células – sólo uno. Por lo tanto, un máximo de una ranura puede ser un valor de 0 a 11111111. Vamos a traducir el número máximo de entradas en la forma habitual.
X = 1 × 2 ⁷ + 1 × 2 ⁶ + 1 × 2 ⁵ + 1 × 2 ⁴ + 1 × 2 ³ + 1 × 2 ² + 1 × 2 ¹ + 1 × 2 ⁰ = 1 × febrero ^8-1 = 255 .

Ahora vemos que en una celda de memoria puede ser posicionado de 0 a 255. Sin embargo, esto sólo se aplica a número entero no negativo. Si el equipo tendrá que registrar un valor negativo, todo va un poco diferente.

los números negativos

Ahora vamos a ver cómo la representación de números en el ordenador, si son negativas. Para la escritura de un valor que es menor que cero, asignado dos células de memoria, o 16 bits de información. Por lo tanto 15 pase por debajo del número en sí, y la primera (más a la izquierda) bit está dada por la marca correspondiente.

Si la cifra es negativa, se registra, "1", si es positivo, entonces "0". Para facilitar la memorización, se puede dibujar la siguiente analogía: si el signo es, a continuación, poner 1 si no lo es, entonces nada (0).

Los 15 bits restantes de información se les asigna un número. Al igual que en el caso anterior, se puede poner un máximo de quince unidades en ellos. Cabe señalar que la entrada de números negativos y positivos es significativamente diferente de la otra.

Con el fin de acomodar las 2 células de memoria es mayor que cero o igual a, un llamado código directo. Esta operación se realiza de la misma manera como se describió anteriormente, y el máximo A = 32766, cuando se utiliza la notación decimal. Sólo quiero señalar que en este caso, "0" se refiere a lo positivo.

ejemplos

Representación de números enteros en la memoria del ordenador no es una tarea tan difícil. Aunque es un poco más complicado cuando se trata de un valor negativo. Para registrar el número de los cuales es menor que cero, usando un código adicional.

Para conseguirlo, la máquina produce una serie de operaciones auxiliares.

1. Primero registrado módulo de un número negativo en notación binaria. Es decir, el equipo recuerda una similar pero positivo.
2. Entonces, una memoria invirtiendo cada bit. Para este fin, todas las unidades se sustituyen por ceros y viceversa.
3. Añadimos un "1" para el resultado. Este será el código adicional.

Este es un claro ejemplo. Supongamos que tenemos un número de X = – 131. En primer lugar, obtener el módulo | X | = 131 se convierte después en un sistema binario y un registro de 16 células. Obtenemos X = 0000000010000011. Tras invertir X = 1111111101111100. Adición a esto de "1" y obtener el código inverso X = 1111111101111101. Para la grabación de una celda de memoria de 16 bits es el número mínimo de X = – (2 ¹⁵⁾ = – 32,767.

anhela

Como se puede ver, la representación de los números reales en un ordenador no es tan difícil. Sin embargo, la discusión de la gama puede no ser suficiente para la mayoría de las operaciones. Por lo tanto, con el fin de acomodar un gran número de ordenador asigna celda de memoria 4, o 32 bits.

El proceso de grabación no difiere de la presentada anteriormente. Así que sólo nos damos un rango de números que se pueden almacenar en este tipo.

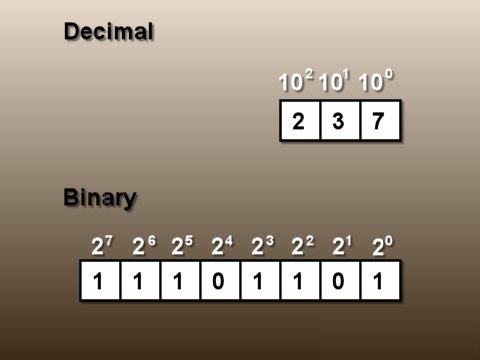
X _max = 2147483647.

X _min = – 2147483648.

Los valores de datos en la mayoría de los casos suficiente para grabar y para realizar operaciones sobre los datos.

Representación de los números reales en un ordenador tiene sus ventajas y desventajas. Por un lado, este método hace que sea más fácil de realizar operaciones entre los valores enteros, que acelera en gran medida el procesador. Por otra parte, este rango no es suficiente para resolver la mayoría de problemas en la economía, física, aritmética y otras ciencias. Así que ahora nos fijamos en otro método para sverhvelichin.

punto flotante

Esta es la última cosa que necesita saber acerca de la representación de los números en un ordenador. Dado que no hay un problema de determinar la posición de una coma en ellos, para acomodar tales números en un ordenador utilizado por la forma exponencial al escribir fracciones.

Cualquier número se puede representar de la siguiente forma X p = m * ^n. Donde m – es el número de mantisa, p – radix y n – el número de orden.

Para estandarizar los números de coma flotante utilizado grabación siguiente condición, según la cual el módulo de mantisa debe ser mayor que o igual a 1 / n y menor que 1.

Vamos número 666.66 se da. Vamos a darle a la forma exponencial. En x = 0.66666 * ¹⁰ de marzo. P = 10 y n = 3.

En el almacenamiento de valores de coma flotante por lo general asignado 4 u 8 bytes (32 bits o 64). En el primer caso se llama el número de precisión simple, mientras que el segundo – un doble precisión.

De los 4 bytes asignados para el almacenamiento de los números, 1 (8 bits) se dan a continuación en los datos de procedimiento y su signo, y 3 bytes (24 bits) para almacenar la mantisa dejar su huella y en los mismos principios que para los valores enteros. Sabiendo esto, podemos hacer algunos cálculos sencillos.

El valor máximo de n = ² 1111111 127 = ^10. En función de ello, podemos obtener la máxima cantidad de números que se pueden almacenar en la memoria del ordenador. X = ^2,127. Ahora podemos calcular la mantisa máximo posible. Será igual a 2 ²³ – 1 ≥ 2 ²³ = 2 ^{(10 x 2,3)} ≥ 1,000 ^2,3 = 10 ^{(3 x 2,3)} ≥ 10 ^séptimo. Como resultado, se obtiene un valor aproximado.

Ahora, si combinamos tanto del cálculo, obtenemos el valor que se puede almacenar sin pérdida de 4 bytes de memoria. Será igual a X = 1,701411 * 10 ^38. Los dígitos restantes se descartan, ya que le permite tener una precisión del método de grabación.

doble precisión

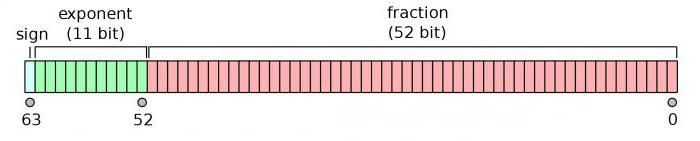
Dado que todos los cálculos se han pintado y se explica en el párrafo anterior, aquí nos dirá todo muy breve. Para los números de doble precisión son generalmente asignados 11 bits para el orden y su signo, así como 53 bits para la mantisa.

1111111111 n = ² 1023 = ^10.

M = ^{2 52 -1 = 2 (10 *} 5,2) = 1,000 5,2 = 10 15.6 . Redondeadas y obtener el número máximo = 2 X ^1.023 hasta "m".

Esperamos que la información sobre la representación de números enteros y números reales en el equipo, hemos proporcionado, es útil en la formación y será un poco más claro que lo que se suele escribir en los libros de texto.