Problemas sobre el área de la plaza y mucho más

Una plaza tan increíble y familiar. Es simétrico respecto a su centro y ejes dibujados a lo largo de las diagonales ya través de los centros de los lados. Y buscar el área de un cuadrado o su volumen no hace mucho esfuerzo. Especialmente si se conoce la longitud de su costado.

Algunas palabras sobre la figura y sus propiedades

Las dos primeras propiedades están relacionadas con la definición. Todos los lados de la figura son iguales entre sí. Después de todo, el cuadrado es el cuadrilátero derecho. Y necesariamente todos los lados son iguales y los ángulos tienen el mismo valor, es decir – 90 grados. Esta es la segunda propiedad.

El tercero está relacionado con la longitud de las diagonales. También son iguales entre sí. Y se cruzan en ángulos rectos y en los puntos del centro.

Una fórmula en la que sólo se usa la longitud lateral

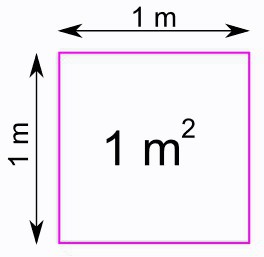
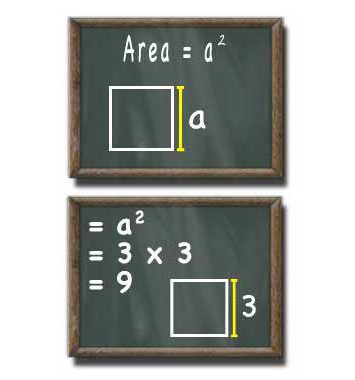
Primero sobre la designación. Para la longitud del lado, es costumbre elegir la letra "a". Entonces el cuadrado del cuadrado se calcula por la fórmula: S = a ² .

Se obtiene fácilmente de la conocida para el rectángulo. En ella, la longitud y el ancho se multiplican. Para un cuadrado, estos dos elementos son iguales. Por lo tanto, el cuadrado de esta cantidad aparece en la fórmula.

La fórmula en la que aparece la longitud de la diagonal

Es la hipotenusa en el triángulo, cuyas patas son las patas de la figura. Por lo tanto, podemos utilizar la fórmula del teorema de Pitágoras y derivar una igualdad en la que el lado se expresa a través de la diagonal.

Realizando tales transformaciones simples, se obtiene que el cuadrado del cuadrado a través de la diagonal se calcula mediante la siguiente fórmula:

S = d _ {2} / 2 . Aquí la letra d denota la diagonal del cuadrado.

Fórmula alrededor del perímetro

En esta situación, es necesario expresar el lado a través del perímetro y sustituirlo en la fórmula de área. Puesto que hay cuatro lados de la figura, el perímetro tendrá que ser dividido por 4. Éste será el valor del lado, que puede entonces ser substituido en el inicial y el área del cuadrado.

La fórmula en forma general es la siguiente: S = (P / 4) ² .

Tareas de liquidación

No. 1. Hay un cuadrado. La suma de sus dos lados es de 12 cm Calcular el área del cuadrado y su perímetro.

La solución. Dado que la suma de los dos lados se da, usted necesita saber la longitud de uno. Puesto que son los mismos, el número conocido debe ser simplemente dividido en dos. Es decir, el lado de esta figura es de 6 cm.

Entonces su perímetro y área se pueden calcular fácilmente a partir de las fórmulas antedichas. El primero es de 24 cm y el segundo de 36 cm ² .

Respuesta. El perímetro del cuadrado es 24 cm, y su área es 36 cm ² .

No. 2. Averigüe el área del cuadrado con un perímetro de 32 mm.

La solución. Es suficiente sustituir el valor perimetral por la fórmula anterior. Aunque primero se puede conocer el lado de la plaza, y luego su área.

En ambos casos, las acciones primero serán seguidas por división, y luego elevando a una potencia. Los cálculos simples llevan al hecho de que el área del cuadrado presentado es de 64 mm ² .

Respuesta. El área requerida es 64 mm ² .

El lado de la plaza es de 4 dm. Dimensiones del rectángulo: 2 y 6 dm. ¿Cuál de las dos figuras tiene más área? ¿Cuánto?

La solución. Sea el lado del cuadrado denotado por la letra a ₁ , luego la longitud y anchura del rectángulo a ₂ y ₂ . Para determinar el área de un cuadrado, el valor de un ₁ debe ser cuadrado, y el rectángulo se multiplica por un ₂ y por ₂ . Es fácil.

Resulta que el cuadrado del cuadrado es 16 dm ² , y el rectángulo es 12 dm ² . Obviamente, la primera cifra es mayor que la segunda. Esto es a pesar de que son iguales, es decir, tienen el mismo perímetro. Para comprobar, puede contar los perímetros. En la plaza, el lado debe ser multiplicado por 4, será de 16 dm. En el rectángulo, doblar los lados y multiplicar por 2. Habrá el mismo número.

En la tarea todavía es necesario responder, en cuántas áreas difieren. Para hacer esto, un número más pequeño se resta de un número más grande. La diferencia es de 4 dm ² .

Respuesta. Las áreas son 16 dm ² y 12 dm ² . En la plaza es más de 4 dm ² .

El problema de la prueba

Condición. El cuadrado se construye sobre la pierna de un triángulo rectángulo isósceles. A su hipotenusa se construye altura sobre la que se construye otra plaza. Demuestre que el área de la primera es dos veces mayor que la segunda.

La solución. Introducimos la notación. Sea el catete igual a a, y la altura a la hipotenusa, x. El área del primer cuadrado es S ₁ , el segundo es S ₂ .

El cuadrado del cuadrado construido en la pierna es fácil de calcular. Resulta ser un ² . Con el segundo valor, todo no es tan simple.

Primero, usted necesita saber la longitud de la hipotenusa. Para esto, la fórmula del teorema de Pitágoras es útil. Las transformaciones simples llevan a la siguiente expresión: a√2.

Dado que la altura en un triángulo isósceles dibujado a la base es también una mediana y una altura, divide un gran triángulo en dos triángulos rectos isósceles iguales. Por lo tanto, la altura es la mitad de la hipotenusa. Es decir, x = (a√2) / 2. Por lo tanto, es fácil averiguar el área S ₂ . Se obtiene como 2/2.

Obviamente, los valores registrados difieren exactamente por un factor de dos. Y el segundo es un número de veces más pequeño. Como se requiere para probar.

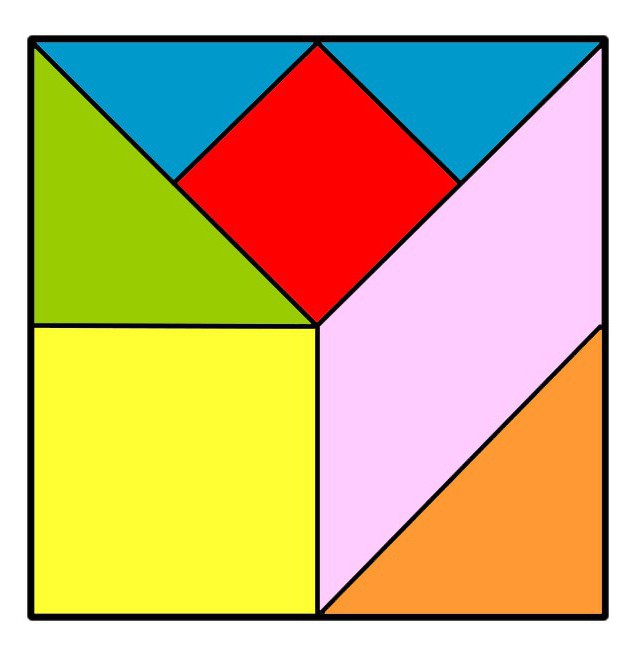
Un rompecabezas inusual – tangram

Está hecho de un cuadrado. Es necesario cortarla en varias formas según ciertas reglas. El total de piezas debe ser 7.

Las reglas suponen que durante el juego se usarán todos los detalles resultantes. De éstos, usted necesita hacer otras formas geométricas. Por ejemplo, un rectángulo, un trapecio o un paralelogramo.

Pero es aún más interesante cuando se obtienen siluetas de animales u objetos de las piezas. Y resulta que el área de todas las figuras derivadas es igual a la del cuadrado inicial.